Hofstadter的非线性递推数列
by
at 2013-01-14 10:44:27
original http://www.matrix67.com/blog/archives/5152
在著名奇书 Gödel, Escher, Bach: An Eternal Golden Braid 的第五章中,为了展现出递推序列的神奇之处,作者 Douglas Hofstadter 定义了这么一个递推序列: G(n) = n - G(G(n - 1)) ,其中 G(1) = 1 。这个序列的前 30 项如下:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| G(n) | 1 | 1 | 2 | 3 | 3 | 4 | 4 | 5 | 6 | 6 | 7 | 8 | 8 | 9 | 9 | 10 | 11 | 11 | 12 | 12 | 13 | 14 | 14 | 15 | 16 | 16 | 17 | 17 | 18 | 19 |
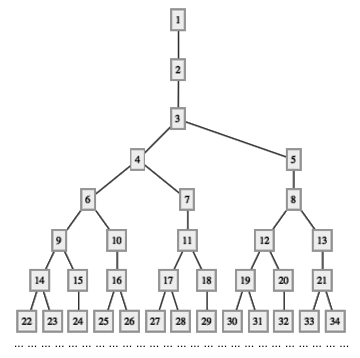
这个数列通常被称作 Hofstadter G-sequence 。它有什么特别的地方呢?如上图,如果把每个标号为 n 的结点都连接到标号为 G(n) 的结点下方,这样的话你将会得到一棵树。从第二行开始算起,各行的结点个数依次为 1, 1, 2, 3, 5, 8, 13, ... 正好是著名的 Fibonacci 数列(头两个数都是 1 ,从第三个数开始,每个数都是前两个数之和)。如果我们把第 i 个 Fibonacci 数记作 Fi 的话,上面的规律可以重新表述为:当 n ≥ 2 时,这棵树的第 n 行的结点总个数为 Fn-1 。另外,这棵树的前 n 行的结点总数(也就是第 n 行最右边那个结点的编号)正好等于 Fn+1 ,也是一个个的 Fibonacci 数。对照上面两个事实,你会惊奇地发现,莫非 F1 + F2 + ... + Fn-1 + 1 总是等于 Fn+1 ?事实的确如此,上面这个式子对于所有大于等于 2 的正整数 n 均成立。
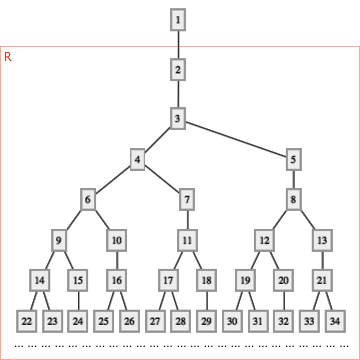
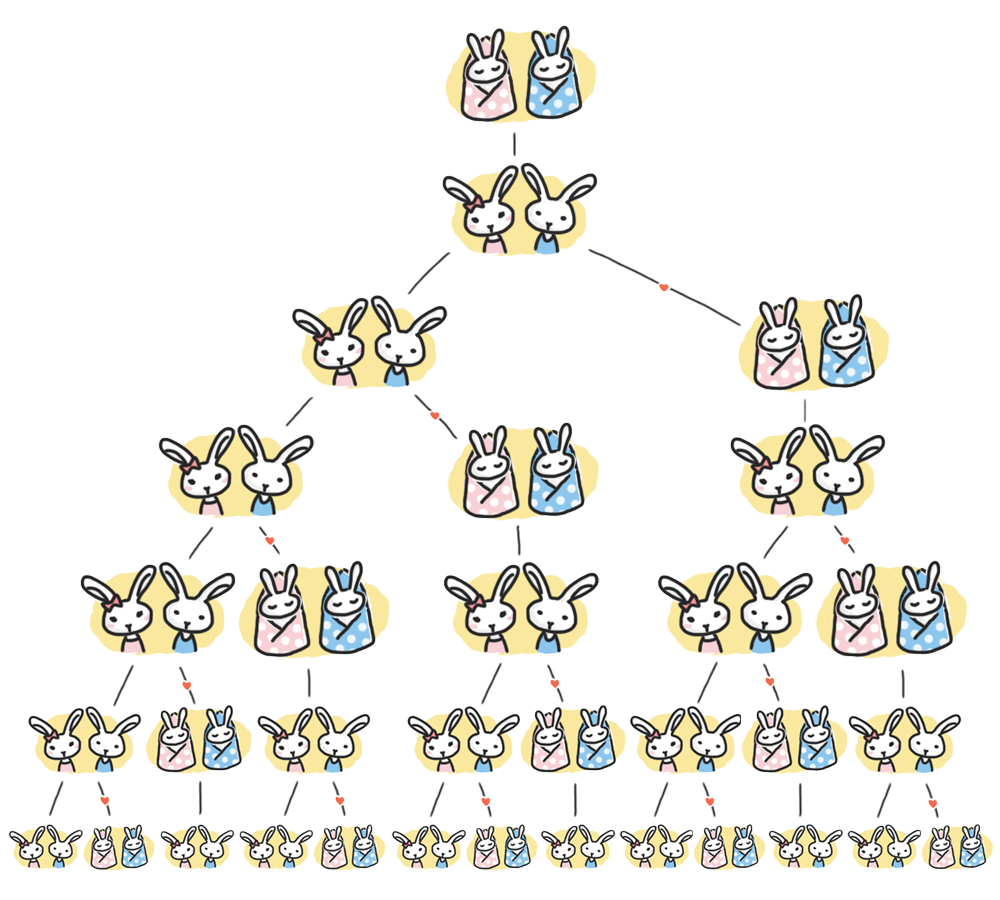
这棵树本身还有别的来头。现在,让我们去掉树中最顶上的那个结点,只保留红色方框里的部分。不妨把这部分的图叫做图 R 。有读者发现图 R 很眼熟吗?它正是经典的“兔子问题族谱图”。假如每一对刚生下的幼兔都会在一个月之后变为成兔,并且在此后的每个月里都会生一对新的兔子。如果刚开始有一对幼兔,那么接下来的各个月里将会有多少对兔子?第一个月,就只有一对兔子;第二个月,还是只有一对兔子(不过已经长大了);第三个月,这对兔子生了一对,于是变为两对兔子;第四个月,这对兔子又生出了一对,于是变为三对兔子。到了第五个月,情况变得有些复杂了,第三个月出生的兔子已经长大了,因而此时一共有了两对成兔。它们将各产生一对新的兔子,从而让第五个月的兔子总数变为五对。继续往下绘制“兔子族谱图”,得到的图形(如下图,感谢 Geek 小美女 localhost_8080 带来的插图)将会和图 R 一模一样。各月的兔子对数形成了 Fibonacci 数列: 1, 1, 2, 3, 5, 8, 13, ... 。
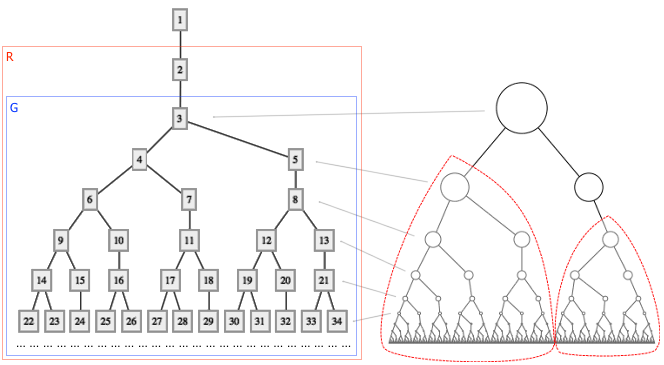
现在,让我们把图 R 中的最上面那个结点也去掉,只看图中蓝色方框内的部分。不妨把这部分的图叫做图 G 。图 G 具有一种让人更加震撼的结构:去掉 3 和 5 这两个结点后,你将会得到两棵分离的子树,这两棵子树的形状和整个图 G 完全一样,如右图所示。换句话说,图 G 是由它自身的两个拷贝高低错落地拼在一起得到的。 Hofstadter 在书里给出了一个更帅的描述:
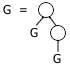
现在,大家看到了同一棵树的好几种不同的描述方法,这些描述方法互相之间都是有联系的(其中有一些是非常明显的)。同时,每一种描述方法都给出了一个新的角度,来解释这棵树和 Fibonacci 数之间的联系。
回到数列 G 本身,它也有很多漂亮的等价定义。
任何一个正整数都可以唯一地表示成若干个两两不同并且两两不相邻的 Fibonacci 数之和。例如, 28 就可以写成 21 + 5 + 2 ,其中 21 、 5 和 2 是三个不同的 Fibonacci 数,并且它们是两两不相邻的。注意,为了把 28 写成若干个不同的 Fibonacci 数之和,我们可能还有一些其他的方法,比方说 28 = 13 + 8 + 5 + 2 ,但这里面包含有相邻的 Fibonacci 数,因而是不允许的。给定一个正整数后,为了找到满足要求的分解方案,我们可以简单地采用“贪心算法”:每次都选择尽可能大的 Fibonacci 数即可。例如,最大的不超过 28 的 Fibonacci 数是 21 ,选了 21 之后,我们就还剩下 7 ;最大的不超过 7 的 Fibonacci 数是 5 ,于是接下来我们选择 5 ,剩下一个 2 ;最大的不超过 2 的 Fibonacci 数就是 2 ,于是选完 2 之后,符合要求的分解方案就找到了: 28 = 21 + 5 + 2 。为什么这种算法得到的分解方案是符合要求的,以及为什么不会有其他满足要求的分解方案,可以参见 Wikipedia 的相关条目。这种用不重复并且不相邻的 Fibonacci 数之和表示正整数的方法就叫做正整数的 Zeckendorf 表达。好了,有趣的事情出现了,如果把正整数 n 的 Zeckendorf 表达中的每一个 Fibonacci 数都替换成它在 Fibonacci 序列中的前一个数,就会得到 G(n) !例如, 28 = 21 + 5 + 2 ,把 21 、 5 、 2 分别替换成小一号的 Fibonacci 数,即 13 、 3 、 1 ,重新加起来便得到 13 + 3 + 1 = 17 ,这正好是 G(28) 的值!这可以看作是数列 G 的一个等价的定义。
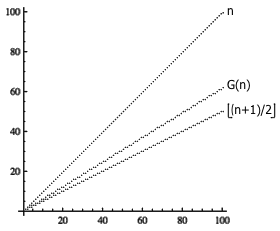
观察数列 G ,容易看出很多其他的性质。例如,数列 G 从 1 开始逐渐递增,序列中的每个数要么出现了一次,要么出现了两次。考虑两个极端情况,数列 1, 2, 3, 4, 5, 6, ... 将会是一个斜率为 1 的线性递增数列,数列 1, 1, 2, 2, 3, 3, 4, 4, ... 则将是一个斜率为 0.5 的线性递增数列。因此,数列 G 也是线性递增的,平均增长速度将会介于 1 和 0.5 之间。那么,数列 G 的平均增长速度究竟是多少呢?为此,我们画出 G(n) / n 的图像,结果非常明确: G(n) / n 趋近于 0.618 附近的一个数,这让我们立即联想到黄金比例。
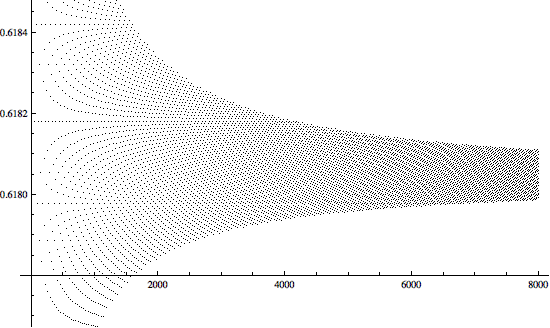
也就是说,数列 G 的平均增长速度是 (√5 - 1) / 2 ?在 1984 年的一篇论文中, Downey 和 Griswold 证明了,事实上对于所有的 n , G(n) 总是等于 ⌊ (n + 1) · (√5 - 1) / 2 ⌋ ,其中 ⌊ x ⌋ 表示不超过 x 的最大整数。这可以看作是 G(n) 的另一个等价的定义。可见,数列 G 确实在以 (√5 - 1) / 2 的速度增长。
故事远远没有结束。如果修改一下数列 G 的定义,我们又会得到什么呢?在那本庞大而诡异的奇书中, Hofstadter 定义了 G(n) 之后,立即介绍了一个新的数列: H(n) = n - H(H(H(n - 1))) ,其中 H(1) = 1 。注意它和 G(n) 的区别:仅仅是在递推时多嵌套了一层。新的序列的前 30 项如下:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| G(n) | 1 | 1 | 2 | 3 | 4 | 4 | 5 | 5 | 6 | 7 | 7 | 8 | 9 | 10 | 10 | 11 | 12 | < |