不可思议的箱子:你的一生就在里面
by
at 2011-06-29 19:00:00
original http://www.guokr.com/article/48357/
如果有人说,你的一生其实就如同被装在一个箱子里面,你会相信吗?你的一生,不会像广告所说的那样“精彩无极限”,我们每天能看到的图像和听到的声音,其可能性其实只是有限多种。
这是为什么?让我们先从电影说起吧。
图像
每个人都或多或少都看过一些高清电影,比如说一部1080p(1080p:垂直方向1080行逐行扫描合成一帧图像)的《致命魔术》。它的分辨率为1920*1080,也就是说这样的一部电影中的任意一个镜头都含有2073600≈2.1M个像素点。在常用的视频格式中,这样的画质非常清晰,完全能够满足视觉要求。另一方面,科学研究表明,人眼能够辨识大约一千万种颜色。让我们做一个合理而宽泛的假设:每一个像素都有可能呈现出这么多种颜色,那么通过数学计算可以得知,存在且仅存在 10M 2.1M 种不重样的静态图像。不论是前年的《变形金刚》绚丽剧照还是十年后的菲利普奖的获奖作品,都包含在内。
而在电影视频及数字视频上,每一帧都是静止的图像,快速连续地显示帧便形成了运动的假象。每秒钟帧数越多,所显示的动作就会越流畅。通常,一秒钟30帧的速度已经足够让眼睛受骗,使人们在脑海中形成流畅的动态画面。于是,我们在一秒钟之内能看见的流畅动画大概就有且只有 10M 2.1M³⁰ 种这么多(这里以时间秒来作为考量单位)。这个数字大约当于 10 10⁶⁰ 那么多,庞大,却是有限的。
声音

看电影总得有声音吧——一句广告词说得好:没声音,再好的戏也出不来。在信息论上,我们有一个著名的“奈奎斯特-香农采样定理”,大概陈述是这样的:
如果信号是带限的,并且采样频率高于信号带宽的一倍,那么,原来的连续信号可以从采样样本中完全重建出来。
人的耳朵大概能听见20Hz到20000Hz的声音。在这样的频率下,我们只需要使用40kHz的采样频率便能满足定理的要求。实际上一张CD使用的采样率是44.1kHz。为了简单起见,我们不妨假设视频的音效和一张CD的音效差不多。44.1kHz意味着我们每秒钟要采集44100个声音样本,而每一个样本通常都需要占用16bit的空间,那么每秒钟就会录制16×44100=705600≈0.71M bit。于是可以算出,总共有 2 0.17M 种不同的持续1s的声音,同样是有限的。
视频

将声音和图像联系起来就是视频。那么不同的一秒钟视频的总数就是 10M 2.1M³⁰ * 2 0.17M !通常,一部电影时长有几个小时,假设一部电影时长不超过两个半小时,这些电影也一定由前述那些不同画面与不同声音搭配而成。那么时长不超过两个半小时的电影总数就是:
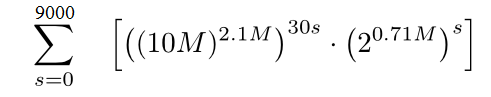
我暂时不知道怎么样才能简单地表达出这个式子的结果,因为这个数字大到难以想象,甚至是它的位数都大到难以想象。不过可以确定的是它仍然是有限的。
人生其实就在一个大箱子里
理论上说,给我足够的时间和资源,我就能够造出所有可能的电影。仿佛所有的电影然都被放在一个硕大无比的箱子里,这个箱子里的电影有《狮子王》,《肖申克的救赎》等等。事实上它还包括了所有未来将会拍摄的电影!
望望远处的绿叶,听听周围的声音。
是不是突然觉得你所听见的、看见的综合起来,其实和一部很长的电影并无二致?是的,或许我们的眼睛像素比1080p的更高,或许我们的耳朵采样率比一张CD的更高,但是这一点也不影响“电影总数是有限的”这一基本特征。实际上,你这辈子就像在看着一部电影:
你憧憬那精彩的一生,其实就在一个大箱子里。
但是请不要灰心,即使身在果壳之中,我们依然可以成为无限宇宙之王。猴子在有生之年敲不出莎士比亚全集,我们在有生之年却能做出许多创造历史的事情,简单如洗牌都是如此,原因正是:虽为有限,依然难以重复。
每一次洗牌都在创造历史

你知道吗:每一次洗牌,你都在创造历史。
大家打牌时或许会经常有“怎么和上局这么像”、“怎么又是这样”的感觉。想打到一模一样的牌局?如果你认真洗牌,这样的情况几乎永远不会发生。1992 年,Persi Diaconis 和Dave Bayer 的一篇论文中提到, 七次交叉洗牌基本上就能让54张牌所有可能的排列概率均等地出现了(参看 _ 这篇文章 )。你知道 54 张扑克牌的排列共有多少种吗?答案是:
54! = 230843697339241380472092742683027581083278564571807941132288000000000000
也就是大约 2.3 × 10 71 。这是一个非常非常大的数,仅是其数量级就已经接近于整个宇宙的基本粒子总个数了。按照宇宙大爆炸理论,目前宇宙已经有 137 亿岁了,这相当于是 4.3 × 10 17 秒。如果从宇宙诞生开始,每一微秒内都有一个人在洗牌,那么宇宙间发生的总的洗牌次数也不超过 10 24 次。即使这 10 24 次洗牌的结果各不相同,和原来的某次洗牌结果撞在一起的概率也只有 10 的 47 次方分之一。
因此,几乎每一次洗牌, 你都能创造一个历史上从未出现的排列顺序。扑克牌游戏的乐趣,或许正在于此——每一个牌局,都是独一无二的。
看到这里,你还会担心自己的独特会被别人在无意中重复吗?
本文出处: SPIKED MATH COMICS : http://spikedmath.com/420.html